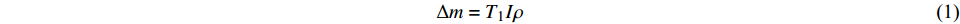Analysis of tipping time characteristics of tipping bucket rain gauge
-
摘要: 在翻斗式雨量计的研究中,由于翻斗旋转速度较快,造成翻斗旋转时间的测量一直以来都是一个难点。利用图像处理中的帧间差分法,结合Matlab软件编程,提出了一种新的翻斗旋转时间测量方法。在此基础上,将该方法应用于4种常用的翻斗式雨量计,在不同的雨强尺度下分别进行试验研究,分析翻斗旋转的时间特性。结果表明:(1)试验中使用的4种单层翻斗式雨量计的翻斗旋转时间在小雨强下不稳定,波动较大;在大雨强下较为稳定,波动较小。(2)JDZ02和CQS·JD02的翻斗旋转时间随雨强的增大而减小,呈较好的线性关系,R2分别为0.99和0.86;JDZ05和CQS·JD05的线性关系不明显,R2均小于0.6。(3)引入数字图像处理中的帧间差分法可以有效获取翻斗旋转的时间特性,并加深对翻斗雨量计的认识。Abstract: During the study of the tipping bucket rain gauge (TBR), objective and sophisticated measurements of the duration of bucket rotation were difficult due to the rapid rotation speed of the bucket. In this paper, a new method of measuring the rotation time of the bucket is presented by using the inter-frame difference algorithm in image processing, combined with MATLAB software programming. The method was applied to four commonly used TBRs, and experimental research was carried out under different rain intensity scales to analyze the time characteristics of bucket rotation. The results show that: (1) The tipping time of the four TBRs used in the experiment is unstable under light rain, and the fluctuations are large; however, it is stable under heavy rain, and the fluctuations are small. (2) The tipping time of the JDZ02 and CQS·JD02 buckets decreases with increasing rain intensity, and shows a good linear relationship, with R2 of 0.99 and 0.86, respectively. The linear relationship between JDZ05 and CQS·JD05 is not obvious, and R2 is less than 0.6. (3) The introduction of the inter-frame difference algorithms during digital image processing can effectively obtain the time characteristics of bucket rotation, and deepen our understanding of the tipping bucket rain gauge.
-
降水是一种最基本的水文现象,降水量是水资源量中最重要的组成部分,因此,精确观测降水量在水资源估算和水文水利计算中有着重要的地位[1-2]。据文献记载,降水量的观测距今已有2 000多年的历史[3]。人类早期的降水测量是将自然降水通过漏斗引入校准容器中进行降水量的测量[4],随后各种种类和用途的雨量器、雨量计应运而生。翻斗式雨量计是一种现代化的测量仪器,具有自动化程度高、获取降水量及时性强、降水量资料易于保存和传输的特点,现已被国内外水文、气象和科研部门广泛应用于降雨观测和科学研究中[5-8]。然而,由于翻斗式雨量计仪器本身不够精密以及人为操作不当的原因,不可避免地会产生仪器误差和测量误差。为尽可能减小这种误差,许多科研机构做了大量研究工作,例如世界气象组织(WMO),不仅对翻斗式雨量计进行了实验室比对试验,还进行了场地比测试验[9-13]。这是WMO首次在实验室条件下组织的雨量计比对试验,主要用于测试不同类型雨量计的工作性能。研究结果表明未经校正的雨量计测量误差较大,而采用正确的校正软件校正过的雨量计则可以准确地测量降水量[6, 9]。因此,降水量观测前,需先对雨量计进行率定。
目前,翻斗式雨量计的率定仍是国内外雨量计研究中的热点问题[10-15],从最初的静态率定,到动态率定,再到现在的智能化率定,逐步趋于成熟和完善。由于翻斗式雨量计翻斗的旋转速度较快,人眼难以捕捉这一过程,常规的测量手段难以达到时间精度要求,所以翻斗的旋转时间测量一直以来都是一个难点且研究严重不足。翻斗旋转时间的研究,有助于进一步了解翻斗在旋转过程中的“水量损失”,以弥补该项研究的不足。Duchon等[16]曾利用高速摄像装置(帧率为500 fps)对翻斗旋转时间进行试验研究,测得翻斗旋转时间约为0.52 s,但试验的次数较少(仅8翻斗),且选取的翻斗式雨量计单一(Met One雨量计),试验结果代表性不足;此外,试验中采用的高速摄像机设备过于昂贵,普通科研工作者难以利用。
因此,本文拟采用数字图像技术(包括视频录制设备和图像处理中的帧间差分法)对国内常见的几种翻斗式雨量计的翻斗旋转时间特性进行系统研究,为设计和生产高精度测量的翻斗式雨量计提供建议与技术支撑。
1. 试验设备及方法
1.1 试验设备
本文选择国内最常见的4种单层翻斗式雨量计进行试验研究,分别是JDZ02,JDZ05,CQS·JD02和CQS·JD05(见图1),基本参数见表1。4种雨量计在不同雨强条件下的翻斗旋转时间特性研究内容包括:(1)研究翻斗启动到水平位置的时间(T1);(2)研究翻斗从启动到另一侧的时间T2(不考虑翻斗的反弹过程);(3)研究不同雨强下,上述两个时间的变化规律。
表 1 4种翻斗式雨量计的基本参数Table 1. Basic characteristics of four types of tipping bucket rain gauges雨量计
类型分辨率/
mm理论单翻斗
感应量/g承雨器
面积/ cm2翻斗旋转的
角度/°JDZ02 0.2 6.28 314.2 26.4 JDZ05 0.5 15.71 314.2 39.4 CQS·JD02 0.2 6.28 314.2 17.5 CQS·JD05 0.5 15.71 314.2 25.0 1.2 试验方法
实验室目前具备一种智能化的翻斗式雨量计率定系统(图2,具备供水、自动计数、防风等功能),可模拟不同雨强对翻斗式雨量计进行试验研究。按GB/T 21978.2—2014 《降水量观测仪器第二部分:翻斗式雨量传感器》规定,在0~4 mm/min雨强范围内,采用5种雨强(0.4,1.0,2.0,3.0,4.0 mm/min)进行对比试验。在模拟降雨的同时,摄像录制设备(帧率为100 fps)记录单个翻斗式雨量计翻斗启动→翻斗达到水平位置→旋转停止的过程。记录完成后,可用软件进行逐帧读取图像画面,可获得翻斗从启动到翻斗水平的时间和翻斗从启动到停止的时间。每种雨强下分别进行20翻斗试验。
翻斗旋转是一个变加速的过程,启动时非常缓慢,然后慢慢加速到水平位置,最后再极快地旋转到另外一侧,完成1次翻斗过程。为了解决这一问题,本文拟采用图像处理中的帧间差分法来判断物体是否运动。帧间差分法常用在交通领域中,判断车辆是否移动,或用在智能监控领域中[17-19]。该方法在本文不做重复叙述,图3为该方法的结果。通过连续增大的SUM值来判断图像中存在运动,即翻斗旋转;无连续增大的区域,说明图像是静止的,翻斗也未旋转。基于帧间差分法,并使用Matlab软件编程来进行图像的逐帧处理,自动保留视频序列中运动的部分,静止的部分则剔除。保留下的运动部分则用来分析翻斗旋转的时间特性。图4为CQS·JD05在4 mm/min雨强下一次翻斗旋转的过程,选取了8个画面进行展示。图4(a)为算法识别的起始状态,记为T=0 s;图4(b)至图4(e)都是翻斗从启动到翻斗到达水平位置的状态;图4(f)为翻斗到达水平位置的时刻;图4(g)为翻斗从水平位置开始向右侧旋转;图4(h)为翻斗旋转到达右侧并触底,完成1次旋转过程。
2. 试验结果与讨论
2.1 视频帧数对试验结果的影响
在试验条件相同的情况下,以JDZ05翻斗式雨量计为例,模拟雨强使翻斗进行20次旋转,用50 fps与100 fps的试验结果进行对比。表2为50 fps视频试验结果与100 fps结果的对比。可见:50 fps的最小值都偏大,但最大值、极差、标准差和平均值都偏大,说明50 fps的视频测量精度不够,100 fps的视频测量精度要更高;另一方面,由于翻斗旋转的速度较快,50 fps视频有的时候不能获取到翻斗到达水平位置的图像,而100 fps的视频基本不会出现这种情况。然而,需要用更高帧率的视频进行拍摄吗?如达到国外学者使用500 fps的高速摄像装置进行视频拍摄[16]。笔者认为答案是否定的,不一定要使用更高的帧率进行拍摄,原因如下:(1)在进行50 fps与100 fps视频对比分析时发现,100 fps的数据文件要比50 fps的大1倍,即处理时间上要多出1倍的时间;(2)在阅读国外学者使用500 fps高速摄像装置所做研究后,发现该学者只分析了8次翻斗旋转的时间。Duchon使用的方法非常新颖,但是工作量却非常少,原因可能在于数据量太大,难以做更多的斗数来分析。综上所述,帧率越高,效率可能并不会提高,只要精度满足了要求即可。故本试验采用100 fps的视频进行拍摄,获取试验数据进行分析。其中,由于该项分析仅对帧率进行对比,且0.4 mm/min雨强进行试验较为耗时,故未设置该雨强进行试验。
表 2 视频帧数对比试验结果Table 2. Comparison of video frame rates帧数/fps 雨强/
(mm·min−1)T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 50 4.0 0.24 0.34 0.10 0.282 0.031 0.30 0.40 0.10 0.350 0.031 3.0 0.26 0.36 0.10 0.300 0.027 0.32 0.42 0.10 0.367 0.030 2.0 0.26 0.34 0.08 0.300 0.029 0.32 0.42 0.10 0.368 0.030 1.0 0.26 0.38 0.12 0.327 0.038 0.34 0.46 0.12 0.394 0.037 100 4.0 0.23 0.30 0.07 0.264 0.021 0.29 0.36 0.07 0.324 0.021 3.0 0.23 0.30 0.07 0.268 0.022 0.29 0.36 0.07 0.328 0.022 2.0 0.22 0.29 0.07 0.257 0.023 0.28 0.35 0.07 0.317 0.023 1.0 0.25 0.32 0.07 0.280 0.032 0.31 0.38 0.07 0.340 0.032 2.2 不同类型翻斗式雨量计翻斗旋转时间特性分析
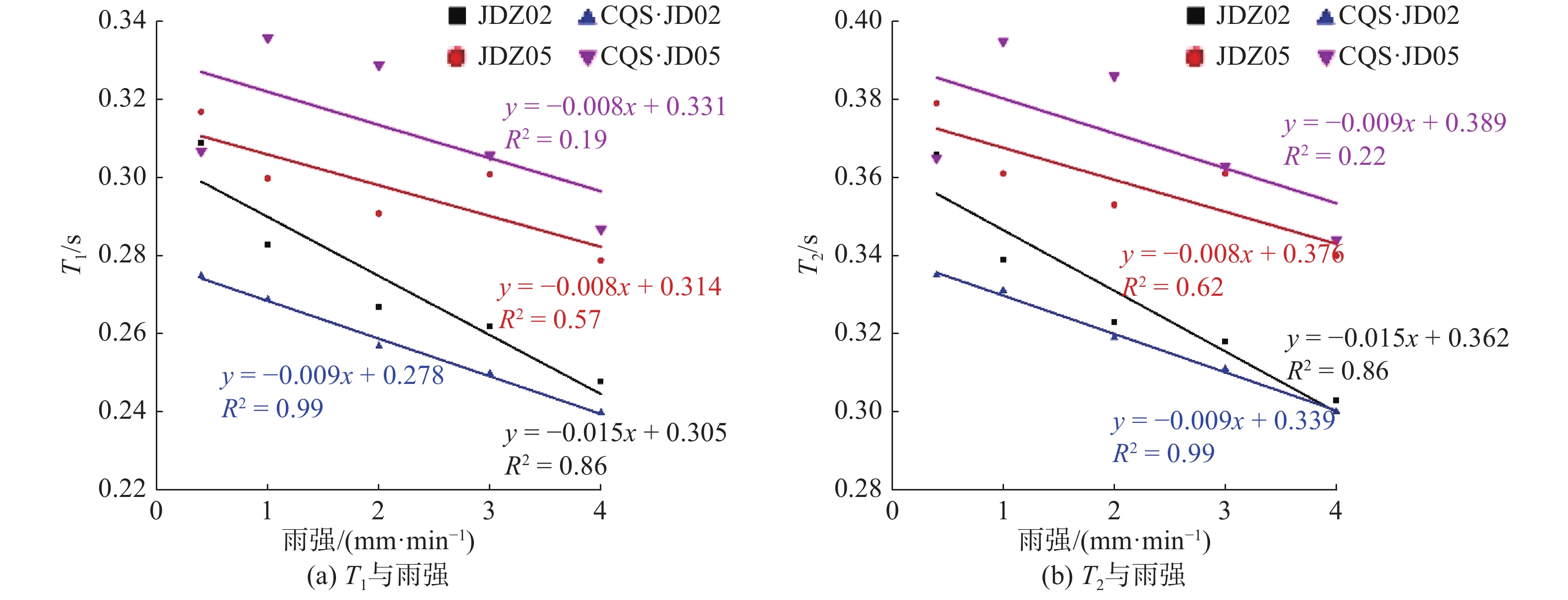
图5为4种类型的翻斗式雨量计旋转时间平均值(T1与T2)与雨强之间的关系。JDZ02和CQS·JD02的平均值随雨强的增大而减小,R2分别为0.99和0.86,有较好的线性关系;JDZ05和CQS·JD05线性关系不明显,R2均小于0.6,相关性较差。Duchon使用Met One翻斗式雨量计进行试验研究,认为翻斗旋转的时间与雨强无关[16]。WMO曾在2006年发表的《WMO laboratory intercomparison of rainfall intensity gauges》报告中指出:“翻斗旋转时间ΔT是雨强的函数”,即雨强与ΔT存在关系,但ΔT很难测量[9]。Marsalek认为翻斗式雨量计的旋转时间在0.3~0.6 s[11],这与本次试验结果接近。
表3是4种类型的翻斗式雨量计在不同雨强下的试验结果,试验斗数均为20斗。由试验数据可得:
表 3 4种类型的翻斗式雨量计在不同雨强下的试验结果Table 3. Test results of four types of tipping bucket rain gauges under different rainfall intensities雨强/
(mm·min−1)JDZ02翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.21 0.29 0.08 0.248 0.023 0.26 0.35 0.09 0.303 0.027 3.0 0.22 0.33 0.11 0.262 0.032 0.27 0.39 0.12 0.318 0.036 2.0 0.22 0.36 0.14 0.267 0.038 0.27 0.42 0.15 0.323 0.041 1.0 0.24 0.44 0.20 0.283 0.046 0.29 0.50 0.21 0.339 0.050 0.4 0.23 0.44 0.21 0.309 0.062 0.28 0.50 0.22 0.366 0.067 雨强/
(mm·min−1)JDZ05翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.25 0.30 0.05 0.279 0.014 0.31 0.36 0.05 0.340 0.015 3.0 0.27 0.36 0.09 0.301 0.024 0.33 0.42 0.09 0.361 0.024 2.0 0.26 0.33 0.07 0.291 0.018 0.32 0.39 0.07 0.353 0.018 1.0 0.26 0.36 0.10 0.300 0.028 0.32 0.42 0.10 0.361 0.028 0.4 0.25 0.39 0.14 0.317 0.034 0.32 0.45 0.13 0.379 0.034 雨强/
(mm·min−1)CQS·JD02翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.20 0.28 0.08 0.240 0.024 0.25 0.34 0.09 0.300 0.028 3.0 0.22 0.28 0.06 0.250 0.026 0.28 0.34 0.06 0.311 0.027 2.0 0.21 0.29 0.08 0.257 0.027 0.27 0.36 0.09 0.319 0.030 1.0 0.23 0.30 0.07 0.269 0.027 0.29 0.37 0.08 0.331 0.029 0.4 0.24 0.31 0.07 0.275 0.065 0.29 0.37 0.08 0.335 0.082 雨强/
(mm·min−1)CQS·JD05翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.24 0.34 0.10 0.287 0.035 0.30 0.40 0.10 0.344 0.037 3.0 0.26 0.36 0.10 0.306 0.040 0.31 0.42 0.11 0.363 0.043 2.0 0.28 0.39 0.11 0.329 0.041 0.33 0.45 0.12 0.386 0.043 1.0 0.28 0.41 0.13 0.336 0.045 0.34 0.47 0.13 0.395 0.045 0.4 0.26 0.37 0.11 0.307 0.038 0.31 0.43 0.12 0.365 0.040 (1)从极差上看,JDZ02和JDZ05在4.0 mm/min雨强下极差最小,在0.4 mm/min雨强下极差最大,极差随雨强的减小而增大。CQS·JD02和CQS·JD05的极差与雨强变化无直接关系,极差随雨强变化不大。
(2)从平均值上看,JDZ02和CQS·JD02的平均值在4.0 mm/min雨强下最小,翻斗旋转最快,在0.4 mm/min雨强下最大,旋转最慢,平均值随雨强的增大而减小。但是对于JDZ05和CQS·JD05两款分辨率为0.5 mm的雨量计来说线性关系不明显,这两款雨量计翻斗旋转时间的平均值在4.0 mm/min雨强下最小,但在0.4 mm/min雨强下并不是最大。
(3)从标准差上看,4款雨量计在4.0 mm/min雨强下标准差最小,在0.4和1.0 mm/min雨强下标准差最大。方差的意义是说明翻斗旋转时间的波动情况,结果表明在4.0 mm/min雨强下,翻斗旋转时间波动最小,在0.4和1.0 mm/min雨强下波动最大。
综上所述,雨量计的翻斗在4.0 mm/min雨强下的旋转时间较为稳定,波动很小,但在0.4 mm/min雨强下的旋转时间却不稳定,波动较大。翻斗式雨量计由于其自身结构的特点,在大雨强时会造成翻斗旋转过程中的“水量损失”,使得记录的水量偏小,造成测量误差。研究翻斗旋转时间特征可为进一步认识翻斗式雨量计的计量误差特性提供理论依据。水量损失的计算见式(1),误差见式(2)。
$$\Delta m = {T_1}I\rho $$ (1) 式中:Δm为翻斗旋转过程中的水量损失;T1为翻斗从启动到水平位置时间;I为雨强;ρ为去离子水的密度(1 g/cm3),本试验采用去离子水,减少密度对试验结果的影响。
$$ {E_{\rm{r}}} = \frac{{{m_1}{\rm{ - }}\left( {{m_1} + \Delta m} \right)}}{{{m_1} + \Delta m}} \times 100\% $$ (2) 式中:Er
为翻斗式雨量计的计量误差;m1为理论上1翻斗的质量。 针对翻斗式雨量计翻斗旋转时间在小雨强下不稳定,波动较大的问题,建议使用虹吸部件。虹吸部件安装在承雨器与翻斗漏斗之间,起调节雨强作用,使得不均匀的降雨能够以相对均匀的方式流入到翻斗中(经过虹吸部件调节后,流入翻斗的雨强会变大),此时调整翻斗对应时刻流入雨强的计量误差使之趋近于0,以减少雨强对翻斗计量的误差[14, 20]。
2.3 翻斗旋转角度对旋转时间影响分析
翻斗式雨量计翻斗的旋转受诸多因素影响,如雨强、翻斗质量、翻斗翻转角度等。本研究主要分析翻斗旋转角度对旋转时间的影响。4种翻斗式雨量计的翻斗旋转角度已在表1中给出,由图5可知,JDZ02和JDZ05两种相同厂家生产的雨量计,翻斗旋转角度越大,T1与T2也越大;对于CQS·JD02和CQS·JD05两种相同厂家生产的雨量计情况也如此。但对于4种翻斗式雨量计来说,并不是翻斗旋转角度越大,旋转时间也就越长,主要的区别在于翻斗的质量不同。
3. 结 语
本文利用图像处理中的帧间差分法,结合Matlab软件编程,提出了一种新的翻斗旋转时间测量方法。为研究翻斗旋转的时间特性,将该方法应用于4种常用的翻斗式雨量计,在不同的雨强尺度下分别进行试验研究:
(1)精确地测量了翻斗式雨量计翻斗的旋转时间,并详细分析了4种翻斗式雨量计在不同雨强下翻斗旋转时间的特性。研究发现,在相同试验条件下,CQS·JD05翻斗旋转时间最长,JDZ05次之,JDZ02再次之,CQS·JD02翻斗旋转时间最短。
(2)对比50 fps与100 fps视频的试验结果发现,100 fps视频试验的效果更好。此外,还与500 fps的试验结果进行对比,认为帧率越高,效率可能并不会提高,只要满足了测量精度要求即可。
(3)引入数字图像处理中的帧间差分法用于翻斗式雨量计的研究,可以获取翻斗旋转的时间特性。同时,可以通过翻斗旋转时间来解释传统率定过程中出现的现象,如水量损失、漏计误差等。
-
表 1 4种翻斗式雨量计的基本参数
Table 1 Basic characteristics of four types of tipping bucket rain gauges
雨量计
类型分辨率/
mm理论单翻斗
感应量/g承雨器
面积/ cm2翻斗旋转的
角度/°JDZ02 0.2 6.28 314.2 26.4 JDZ05 0.5 15.71 314.2 39.4 CQS·JD02 0.2 6.28 314.2 17.5 CQS·JD05 0.5 15.71 314.2 25.0 表 2 视频帧数对比试验结果
Table 2 Comparison of video frame rates
帧数/fps 雨强/
(mm·min−1)T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 50 4.0 0.24 0.34 0.10 0.282 0.031 0.30 0.40 0.10 0.350 0.031 3.0 0.26 0.36 0.10 0.300 0.027 0.32 0.42 0.10 0.367 0.030 2.0 0.26 0.34 0.08 0.300 0.029 0.32 0.42 0.10 0.368 0.030 1.0 0.26 0.38 0.12 0.327 0.038 0.34 0.46 0.12 0.394 0.037 100 4.0 0.23 0.30 0.07 0.264 0.021 0.29 0.36 0.07 0.324 0.021 3.0 0.23 0.30 0.07 0.268 0.022 0.29 0.36 0.07 0.328 0.022 2.0 0.22 0.29 0.07 0.257 0.023 0.28 0.35 0.07 0.317 0.023 1.0 0.25 0.32 0.07 0.280 0.032 0.31 0.38 0.07 0.340 0.032 表 3 4种类型的翻斗式雨量计在不同雨强下的试验结果
Table 3 Test results of four types of tipping bucket rain gauges under different rainfall intensities
雨强/
(mm·min−1)JDZ02翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.21 0.29 0.08 0.248 0.023 0.26 0.35 0.09 0.303 0.027 3.0 0.22 0.33 0.11 0.262 0.032 0.27 0.39 0.12 0.318 0.036 2.0 0.22 0.36 0.14 0.267 0.038 0.27 0.42 0.15 0.323 0.041 1.0 0.24 0.44 0.20 0.283 0.046 0.29 0.50 0.21 0.339 0.050 0.4 0.23 0.44 0.21 0.309 0.062 0.28 0.50 0.22 0.366 0.067 雨强/
(mm·min−1)JDZ05翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.25 0.30 0.05 0.279 0.014 0.31 0.36 0.05 0.340 0.015 3.0 0.27 0.36 0.09 0.301 0.024 0.33 0.42 0.09 0.361 0.024 2.0 0.26 0.33 0.07 0.291 0.018 0.32 0.39 0.07 0.353 0.018 1.0 0.26 0.36 0.10 0.300 0.028 0.32 0.42 0.10 0.361 0.028 0.4 0.25 0.39 0.14 0.317 0.034 0.32 0.45 0.13 0.379 0.034 雨强/
(mm·min−1)CQS·JD02翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.20 0.28 0.08 0.240 0.024 0.25 0.34 0.09 0.300 0.028 3.0 0.22 0.28 0.06 0.250 0.026 0.28 0.34 0.06 0.311 0.027 2.0 0.21 0.29 0.08 0.257 0.027 0.27 0.36 0.09 0.319 0.030 1.0 0.23 0.30 0.07 0.269 0.027 0.29 0.37 0.08 0.331 0.029 0.4 0.24 0.31 0.07 0.275 0.065 0.29 0.37 0.08 0.335 0.082 雨强/
(mm·min−1)CQS·JD05翻斗式雨量计 T1/s T2/s 最小值 最大值 极差 平均值 标准差 最小值 最大值 极差 平均值 标准差 4.0 0.24 0.34 0.10 0.287 0.035 0.30 0.40 0.10 0.344 0.037 3.0 0.26 0.36 0.10 0.306 0.040 0.31 0.42 0.11 0.363 0.043 2.0 0.28 0.39 0.11 0.329 0.041 0.33 0.45 0.12 0.386 0.043 1.0 0.28 0.41 0.13 0.336 0.045 0.34 0.47 0.13 0.395 0.045 0.4 0.26 0.37 0.11 0.307 0.038 0.31 0.43 0.12 0.365 0.040 -
[1] 关铁生, 姚惠明, 许钦, 等. 辽河区极端暴雨特性及其天气成因分析[J]. 水利水运工程学报,2015(2):18-25. (GUAN Tiesheng, YAO Huiming, XU Qin, et al. Characteristics and weather causes of extreme rainstorms in Liaohe River region[J]. Hydro-Science and Engineering, 2015(2): 18-25. (in Chinese) [2] 范梦歌, 刘九夫. 基于聚类分析的水文相似流域研究[J]. 水利水运工程学报,2015(4):106-111. (FAN Mengge, LIU Jiufu. Analysis of hydrologically similar basins based on clustering analysis[J]. Hydro-Science and Engineering, 2015(4): 106-111. (in Chinese) [3] UPTON G J G, RAHIMI A R. On-line detection of errors in tipping-bucket raingauges[J]. Journal of Hydrology, 2003, 278(1/4): 197-212. doi: 10.1016/S0022-1694(03)00142-2
[4] BISWAS A K. Development of rain gages[J]. Journal of the Irrigation and Drainage Division, 1967, 93(3): 99-124.
[5] VASVÁRI V. Calibration of tipping bucket rain gauges in the Graz urban research area[J]. Atmospheric Research, 2005, 77(1/4): 18-28. doi: 10.1016/j.atmosres.2004.12.012
[6] LANZA L, STAGI L. High resolution performance of catching type rain gauges from the laboratory phase of the WMO field intercomparison of rain intensity gauges[J]. Atmospheric Research, 2009, 94(4): 555-563. doi: 10.1016/j.atmosres.2009.04.012
[7] COLLI M, LANZA L G, LA BARBERA P, et al. Measurement accuracy of weighing and tipping-bucket rainfall intensity gauges under dynamic laboratory testing[J]. Atmospheric Research, 2014, 144: 186-194. doi: 10.1016/j.atmosres.2013.08.007
[8] BURT S. British rainfall 1860-1993[J]. Weather, 2010, 65(5): 121-128. doi: 10.1002/wea.603
[9] LANZA L, LEROY M, ALEXANDROPOULOS C, et al. WMO laboratory intercomparison of rainfall intensity gauges[R]. Geneva: WMO, 2006.
[10] HUMPHREY M D, ISTOK J D, LEE J Y, et al. A new method for automated dynamic calibration of tipping-bucket rain gauges[J]. Journal of Atmospheric and Oceanic Technology, 1997, 14(6): 1513-1519. doi: 10.1175/1520-0426(1997)014<1513:ANMFAD>2.0.CO;2
[11] MARSALEK J. Calibration of the tipping-bucket raingage[J]. Journal of Hydrology, 1981, 53(3/4): 343-354. doi: 10.1016/0022-1694(81)90010-X
[12] LIAO M H, LIU J F, LIAO A M, et al. Investigation of tipping-bucket rain gauges using digital photographic technology[J]. Journal of Atmospheric and Oceanic Technology, 2020, 37(2): 327-339.
[13] 廖敏涵, 刘九夫, 廖爱民, 等. 三种JDZ型翻斗式雨量计性能比对实验研究[J]. 水文,2020,40(1):29-34. (LIAO Minhan, LIU Jiufu, LIAO Aimin, et al. Experimental investigation on comparison of three types of JDZ tipping bucket rain gauge[J]. Journal of China Hydrology, 2020, 40(1): 29-34. (in Chinese) doi: 10.1016/0022-1694(78)90013-6 [14] OVERGAARD S, EL-SHAARAWI A H, ARNBJERG-NIELSEN K, et al. Calibration of tipping bucket rain gauges[J]. Water Science and Technology, 1998, 37(11): 139-145. doi: 10.2166/wst.1998.0454
[15] SHEDEKAR V S, KING K W, FAUSEY N R, et al. Assessment of measurement errors and dynamic calibration methods for three different tipping bucket rain gauges[J]. Atmospheric Research, 2016, 178/179: 445-458. doi: 10.1016/j.atmosres.2016.04.016
[16] DUCHON C, FIEBRICH C, GRIMSLEY D. Using high-speed photography to study undercatch in tipping-bucket rain gauges[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(6): 1330-1336. doi: 10.1175/JTECH-D-13-00169.1
[17] PATHAN I, CHAUHAN C. A survey on moving object detection and tracking methods[J]. International Journal of Computer Science and Information Technologies, 2015, 6(6): 5212-5215.
[18] LI W J, YAO J G, DONG T Z, et al. Moving vehicle detection based on an improved interframe difference and a Gaussian model[C]//Proceedings of 2015 International Congress on Image and Signal Processing. Shenyang: IEEE, 2015: 969-973.
[19] WENG M Y, HUANG G C, DA X Y. A new interframe difference algorithm for moving target detection[C]//Proceedings of 2010 International Congress on Image and Signal Processing. Yantai: IEEE, 2010: 285-289.
[20] SIMIĆ M, MAKSIMOVIĆ Č. Effect of the siphon control on the dynamic characteristics of a tipping bucket raingauge[J]. Hydrological Sciences Journal, 1994, 39(1): 35-46. doi: 10.1080/02626669409492718
-
期刊类型引用(2)
1. 郑路,李华,马俊旭,李朝英,杨坤. 翻斗式雨量计现场校验及误差分析与修正. 生态学杂志. 2023(04): 1012-1017 .  百度学术
百度学术
2. 胡春宏,郑春苗,王光谦,张建云,王超,姚檀栋,王焰新,赖明勇,倪广恒,王雨春,张弛,田富强. “西南河流源区径流变化和适应性利用”重大研究计划进展综述. 水科学进展. 2022(03): 337-359 .  百度学术
百度学术
其他类型引用(0)



 Email Alerts
Email Alerts RSS
RSS

 下载:
下载: